I occasionally read Howard Marks’s memo, and in my recent infrequent visit, I have constantly encountered him citing Marc Lipsitch, Professor of Epidemiology at Harvard, that (in Lipsitch’s covid research and in Marks’s money making) there are:

1. facts,
2. informed extrapolations from analogies to other viruses and
3. opinion or speculation.

That is right. Statistician needs some stationarity and smoothlization assumption so as to learn from data— and thereby always place ourselves in the risk of over-extrapolation.

In machine learning, the novelty detector and out-of-distribution uncertainty used be a hotspot especially given its connection to AI safety, and I have followed papers in this area for a while. (I think it is still a hotspot, but I don’t know for sure— indeed if someone tell you that he would be completely sure on the presence or the future, he is completely extrapolation, but anyway, it is fairly to assume the heat of areas does not shrink overnight, so maybe it is still at least a warm spot.)

In part many deep models ignored the parameter uncertainty and is overconfident. But I feel like there is a dangerous tendency that people treat some non-parametric bayesian model as always-right-but-hard-to-fit-model, as if we would never worry about novelty detector and out-of-sample uncertainty if we know how to fit a gaussian process with 10^10 points.

But gp is not immune to extrapolations. Here I generate 2 two-D data (x,y) with x only supported near 1 and 3 (.5 N(1, 0.01) + .5 N(3,0.01)). I could still fit a gp, and it does return results that fit the data in their support.

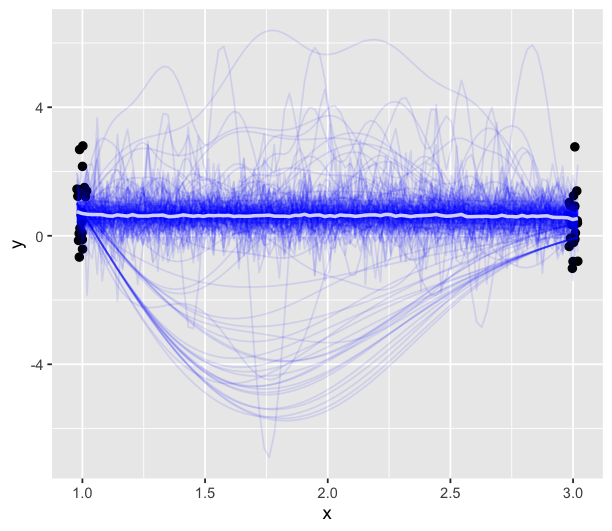
But wait, why is it so sure about what happens in between— there is zero data in the middle! How could you know the f(x) at 2 is identically 0, instead of -20004, or 343583? The model is completely extrapolation.

You could probably guess the fitted length scale is very big— indeed longer than the x span so it effectively becomes a linear regression. It is not wrong, a linear regression can be useful too.

Even worse, such over-confidence is self-confirmed. Wikipedia says “the length scale tells how safe it is extrapolate outside the data span”. It is wrong. It does not tell use how safe it is. The inference in the no-data-zone comes from the prior, which is a mean zero gp, and it is very dangerous, arrogant and reckless if treat that as always the true model and the right uncertainty we are looking for.

Ideally we want a model/inference that goes on strike and yelling at the user when it perceived it is making non-data-ful extrapolation. Of course anything beyond data comes from prior, and prior is just more data, so technically it is as kosher to estimate the posterior outside the data domain by a crazy gp prior as to estimate the empirical density by a delta function — which are two extremes on the spectrum of how we weigh the relative reliance on prior and data. If you do not yell at the empirical process, why should the gp yell at you?

It is not utterly sane to stop this post with the previous question which I do not know the answer. But the main message is clear, gp is not always right. And gp can as over-extrapolating as a linear regression. And in many cases we do not know if the gp we are running is over-extrapolating or not.