Does the E-commerce Giant Fabricated its One-dimensional Data?
Posted by Yuling Yao on Nov 14, 2019.As for the background, there is a giant online retailer company A in county C– I will not mention their names, and I will also not tell the reason why I do not tell their names– has an annual one-day sale event on every Nov 11. And this year its one-day gross merchandise volume (GMV) has reached an all time high to be 268.4 billion CNY (equivalently 38.4 billion USD). However, the release of such data soon evoked a strong public debate on the Internet. In particular, someone accused this e-commerce giant for fabricating the sales data, with a very convincing evidence: he could fit the company’s 2009-2019 data with a quadric regression, with an R square 0.999.
I pulled up the data. It reads:
| Year | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Alibaba Released GMV (100 million CNY) | 0.5 | 9.36 | 52 | 191 | 350 | 571 | 912 | 1270 | 1682 | 2135 | 2684 |
Now we fit a simple linear regression of the sales number $y$ up to quadric predictors y~year+year^2, it is somewhat surprising that the R square is:
\[0.996\]I have zero interest in whether this company has fabricated its own data or not. As said by Fed’s Powell this Wednesday (Nov 13) in his congressional testimony when questioned (It seems he was describing some deep learning too):
It’s very hard to understand (country C), the way the economy works, the way society works. Just accept that it’s really hard to know.
But just out of curiosity, how would a statistician tell if the data is fabricated?
To some extent it seems impossible as the data itself can never whisper “yo, I am fake”. If we have a validation set we could of course have a reasonable hypothesis testing (VAE for example). But to tell if a single realization of data is fake is unsupervised and how is that even possible? In the high level statistics needs some replication, either external or internal, does a single dataset even sound? We are prone to the cliche the “all models are wrong”, are we now in the “all data are wrong” era?
A good example where data do whisper: Bashar al-Assad
Several years ago Andrew pointed out that “it’s pretty obvious the Syria vote totals are fabricated”. The evidence is from the released data:
There’s 11,634,412 valid ballots, and Assad won with 10,319,723 votes at 88.7%. That’s not 88.7%, that’s 88.699996%. Or in other words, that’s 88.7% of 11,634,412, which is 10,319,723.444, rounded to a whole person. All the other percentages in the results are the same way, so given the magnitude of the numbers, it’s evident someone took the total number, used a calculator and rounded.
They are too accurate.
In this example an implicit hypothesis testing based on the fact that the rounding error with one decimals should be uniform (-0.05,0.05), and in this case we get a 0.000004. That is we draw a 0.00008 from a uniform (-1,1). It is too close to 0.
But what if the round error is 0.045867 and someone else would accuse it being too close to 0.045860 (in a one sided test)? The reasoning is essentially multiple testing and why we hate 0 in the first place?
This should be understood as a pre-registered research. When people fabricate records in an inverse way, the rounding error becomes nearly zero so it suffices to test this single default hypothesis.
Of course even with this simple question there is no definite answer. Andrew wrote:
But is this actually fraud? I can’t say for sure, as I don’t know where the numbers purportedly come from. It is possible, for example, that the exact totals are not as reported, and what happened is that one person in the election office computed the vote proportions to the nearest tenth of a percent, and then a different person took these percentages and multiplied them by the total of 11634412 to get the numbers that were reported.
That is right, a Bayesian never assigns a point mass.
So how about the regression
What is the chance that data with size 11 can fit a quadric regression with an R square 0.9996?
Probably NOT p=0.0004.
First, a quadric regression contains 3 predictors including the constant. With 11 data is already prone to overfitting.
Second, when the date ranges different orders of magnitude, the R square is misleading.
Let’s recall what the key assumption of linear regression is:
- Validity. Most importantly, the data you are analyzing should map to the research question you are trying to answer. This sounds obvious but is often overlooked or ignored because it can be inconvenient. . . .
- Additivity and linearity. The most important mathematical assumption of the regression model is that its deterministic component is a linear function of the separate predictors . . .
- Independence of errors. . . .
- Equal variance of errors. . . .
- Normality of errors. . . .
In particular, the equal variance of errors cannot hold in such data. This is not an uncommon mistake in practice. For instance, the measurement error threshold in many medical tests is controlled by “x or y%, whoever is larger”.
If all unmeasured error terms are additive, it render a linear error terms that scales equally for all outcomes. Alternatively a multiplicative error term results in a fixed percentage range, or an additive error with equal variance in the log scale. This is mostly the argument why Andrew suggests you should always do a 1/4-th power transformation (cf. log or Cox transformation with data-dependent power index) for such data.
In other words, if I fit $y$ directly, where $y$ varies several orders of magnitudes, using an equal-scale-variance, the result is mostly driven by the last few terms. With an R square defined as “Explained variation / Total variation” in the linear scale, it mostly depends on the last few terms too.
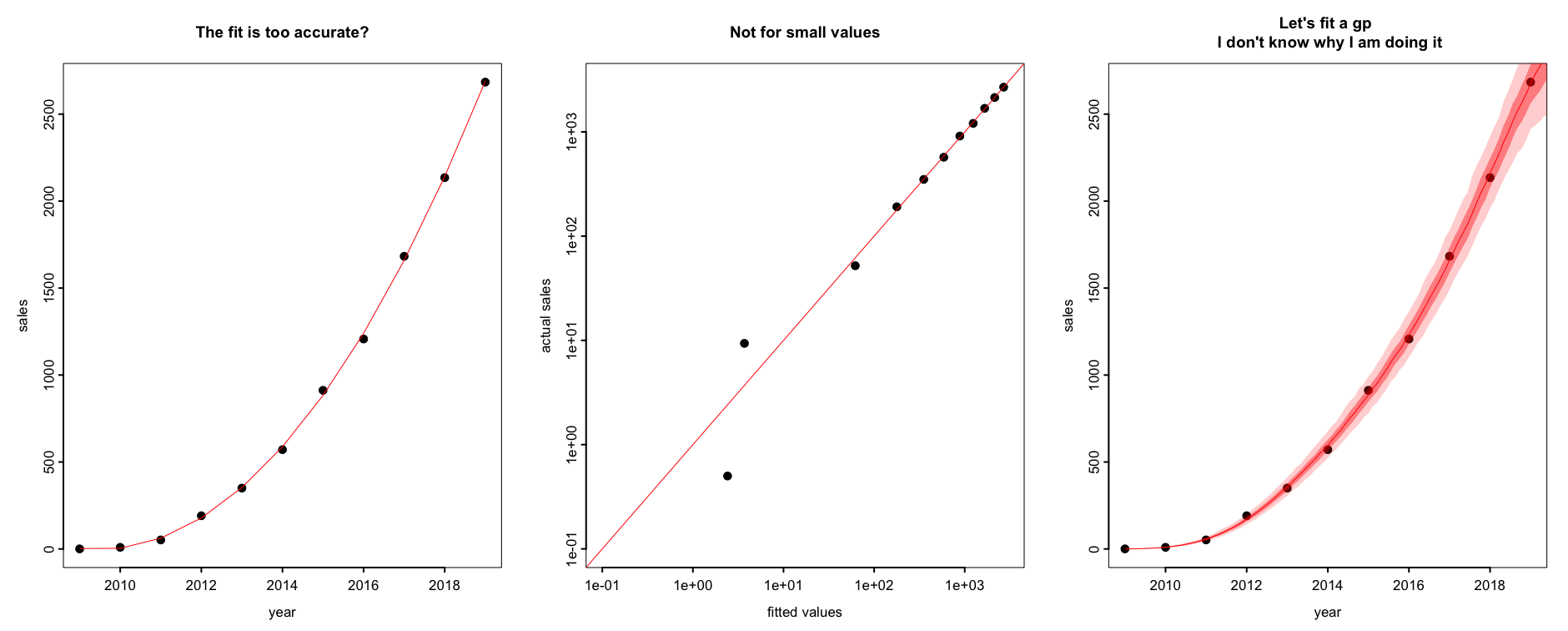
To amplify such small-end effect I plot the actual value vs the prediction value in log scale. Apparently the small end is very inaccurate. With df=3, one could always fit the last few large values well.
Just for curiosity, I also fit the data using a gaussian process but with a 1/4 transformation on $y$ first. Indeed I don’t know why I am doing it other than proving if I or Stan is able to fit a gp. Anyhow the vague message I want to convey there is some variation in the prediction–If gp represents the more correct model– nothing is perfectly predictable from the data per se.
Some theory: How expressive is the class of polynomials?
More theoretically, how good is a polynomial fit in terms of a linear regression? The answer is summarized by the following theorem:
Consider a Holder space $\mathcal{C}^{\alpha}[0,1]$, there exists a constant D that depends only on $\alpha$ such that for any $f \in \mathcal{C}^{\alpha}[0,1]$ that is $\alpha$ smooth and any degree of freedom $k$, there exists a polynomial $P$ of degree of freedom $k$ such that
\[\vert\vert f-P\vert\vert_\infty\leq Dk{^{-\alpha}}\vert\vert f\vert\vert_{\mathcal{C}^{\alpha}}.\]Roughly speaking, the closest polynomial of degree $k$ has an $l_{\infty}$ error $k^{-\alpha}$. Notice the role of the $l_{\infty}$ norm.
As a consequence, we can heuristically show:
\(1-R^2= \frac{ \vert\vert \mathrm{error} \vert \vert_{l_2}^2}{\mathrm{total\ \ variation}} \leq \frac{ \vert\vert \mathrm{error} \vert \vert_{\infty}^2}{\mathrm{total\ \ variation}} \leq \mathcal{O}({k^{-2\alpha}})\) which shrinks quickly (to 0) as $k$ grows. For example, if the smooth index $\alpha$ is 2, then a R squared of $\mathcal{O}(1)$ using a linear predator, it shrinks to $R^2 \approx 0.9999$ using quadric regressions.
Let me take a step back. Even without all the previous discussion on statistical flaws, and even if all numbers fits perfectly in a regression line, one can still argue there is a casual story under the hook– which as I said earlier, is very hard to be either verified or by rejected by data even with further replications if you view them as causal assumptions. But that is fine too, a data is a data, and there are many things that data can not tell.
The bottomline
- R squared might be a misleading measure for such regressions.
- Do a 1/4 transformation please.
- The argument based on such R hat does not prove the potential data-fabrication. “Just accept that it’s really hard to know”.
