I was talking to BenB about how unlucky we (Ben and me) would be amid a looming economic crisis and financial shortage when we were about to enter the job market.

To support my straw-man argument that “we are quite screwed up”, I found that Eisenhower was 39 in 1929, while JFK was 12 — if COVID-19 would have an as serious economic effect as the great depression, then my generation (currently late 20s) would be the same one sandwiched between JFK and Eisenhower.

OK life is still fine without the goal of being POTUS, but I am kinda curious, what is the cohort effect that is induced by a recession in early life? And, more pedantically, if we have to encounter some recession from time to time, which age would be the worst to face it?

I ask this question because I will graduate in 2021, so basically I know I am likely to be the worst. But again, you occasionally need a Stan model to prove your straw-man argument.

I fit a very similar age-period-cohort model as in Yair Ghitza et al. They used it to analyze the generation effect induced by presidential approval rate. Many years ago Yu-Sung and I also utlized a similar model to fit the generation effect of the Chinese people’s happiness— we even copy the title.

For this toy dataset, I collected all presidents’ birth years, and US inflation adjusted GDP. The early historical data is inputed from an estimation of Clio-Infra.

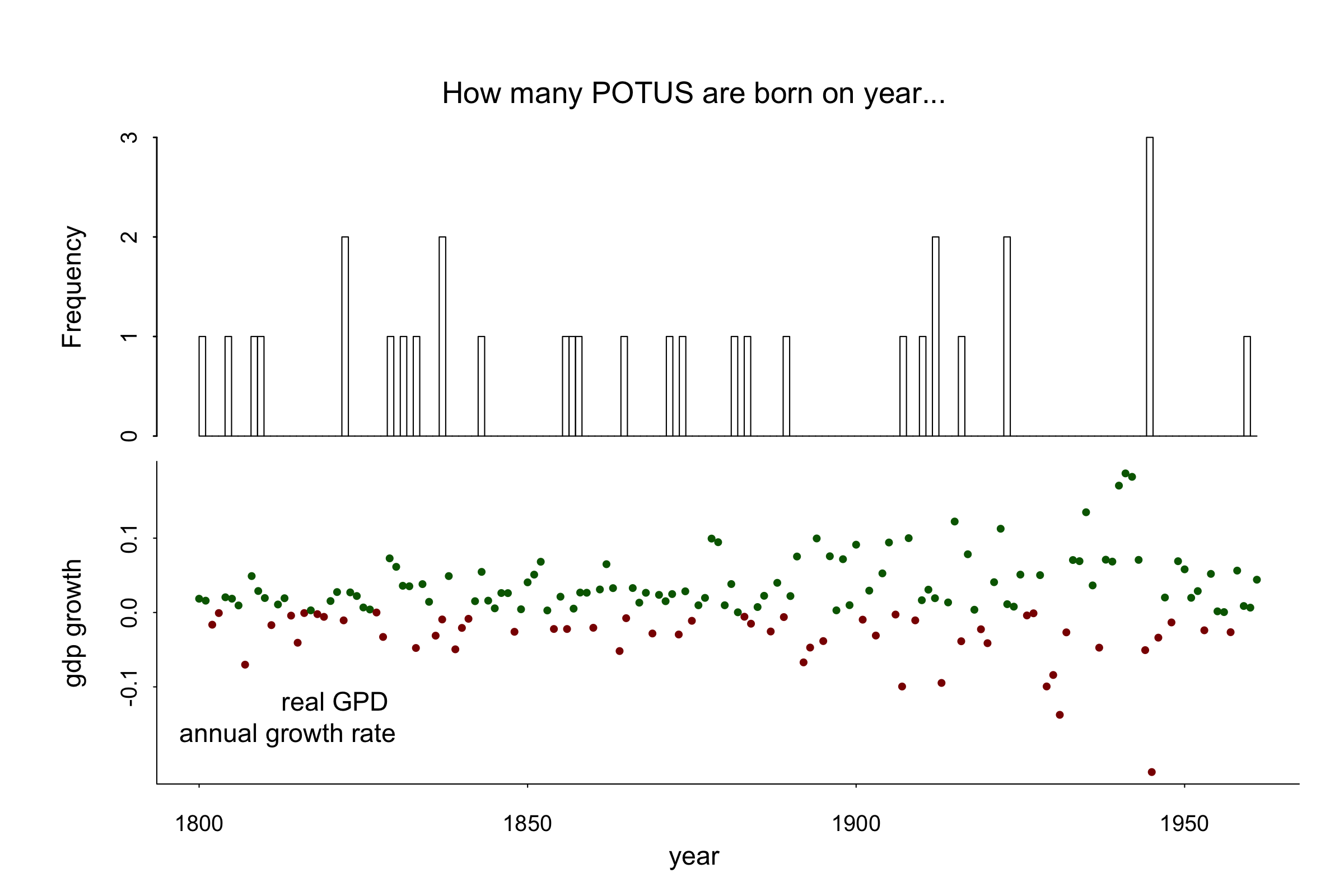
It is tempting to claim the presidents’ birth years are not distributed evenly— until I think it is actually hard to make a precise test for such claim. At first I thought it should be quite rare to see three presidents born in the same year. But suppose I am sampling 45 draws with replacement from year year 1732 (birth year of Washington) to 1961 (Obama), and if each year is equally likely to be sampled, the chance of sampling a prespecified year three times is (45/230)^3, but after a multiple-testing adjustment, the p value is quite big. How about a one-sample Kolmogorov-Smirnov tests:

dgof::ks.test(president_birth_year, ecdf(1732:1961))
D = 0.10918, p-value = 0.8401  

So I guess it is actually distributed quite evenly—no deep states, no conspiracy theory folks! (That said, KS test has too small power and I remember Persi Diaconis has a recent math paper on hypothesis testing on discrete uniform variables. In this dataset you could probably find some better test statistics to reject the null, but that is not my purpose of this post anyway. )

Return to the cohort effect. Let’s assume the gdp’s growth rate, denoted by $x_j$ on year $j$, is accumulated in one’s early life via a age-varying accumulation rate $\gamma_a$ at age $1\leq a \leq A$, I truncate $A=35$ ad-hocly. The generation that was born on year $k$ will receive a total effect

We assume a Poisson observational model with mean $\exp ( \alpha_k + \alpha_0 )$:

Here $y_k$ is the counts of presidents that were born on year k. We smoothlize the estimation by an AR prior $\gamma_i \sim \mathrm{normal}(\gamma_{i-1}, \tau), \tau \sim \mathrm{normal}(0,1)$.

data {
  int<lower=0> A;  // number of ages to accumulate 
  int<lower=0> S; // number of years
  int y[S]; // counts of presidents in that year
  matrix[S,A] growth_at_age; // gdp growth rate
  }
parameters {
  vector<lower=0>[A] gamma;   // age-varying accumulate rate
  real c;
  real<lower=0> tau;
  }
transformed parameters{
 vector[S] agg_effect;  // aggregated cohort effect

 agg_effect=growth_at_age*gamma+rep_vector(c, S);
}
model {
  for(s in 1:S)
  y[s] ~ poisson(exp(agg_effect[s]));
  gamma[1]~normal(0,0.5); 
  gamma[A]~normal(0,0.1);
  for(a in 2:A)
   gamma[a-1]~normal(gamma[a],tau);
  tau~normal(0,1); 
}

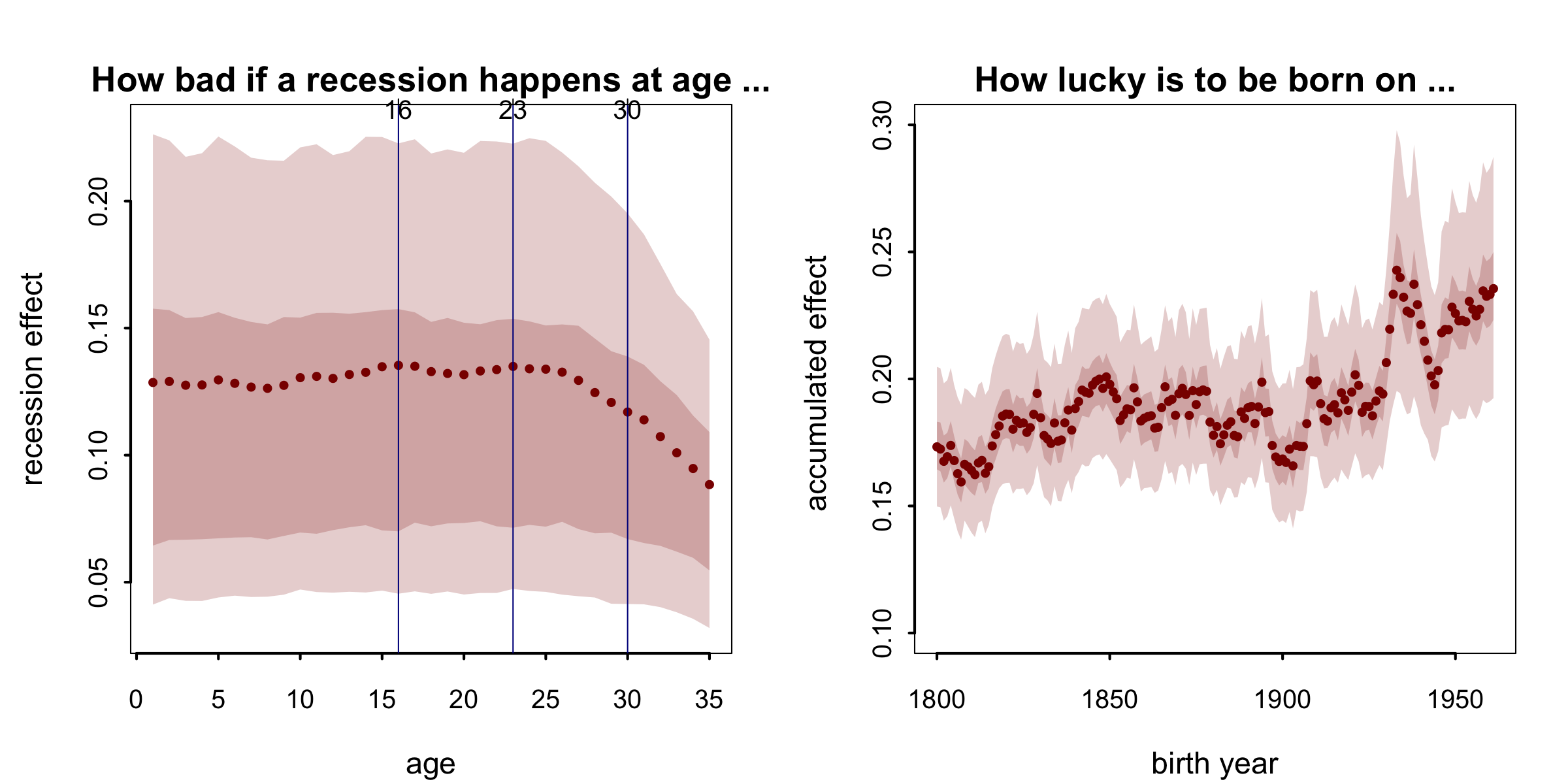
Hmmm, I don’t want to overstate the result, as it is quite a weak effect anyway, plus this is inference based on 45 data points. But basically from the graph, there is a positive relation between how likely people born in certain year will be president and gdp growth rate in their early life. If I am allowed to exaggerate the finding, I will point out there are two local maximums at age 16 and 23 in the posterior mean of $\gamma$, around the middle school and college graduation age, which is probably equivalent to my age now given the inflation—not good for me, folks. For older cohorts (>30), the effect to accumulate is smaller.

The right hand side shows the accumulated cohort effect. In particular people born around 1900 (late in 1929) are less fortunate, and this is in line with a gap of observed POTUS birth year around 1900 in the previous histogram.

In the end I will offer a few counterargument to ease people around my generation who might be worried about the current situation and its long term effect:

1. 45 is a super small sample size.
2. There is nothing causal here analyzed.
3. COVID is real, and more uncertainty is yet to come. History is never stationary.
4. Many model assumptions are horrible. Voting for president is not a multinomial sampling, and there are many other factors should be include.
5. Instead of a global comparison, the local comparison is more important. To have a blessed career, you are competing with Lincoln and Washington, you only need relative advantage than your neighbor generations. Maybe I should fit a spline with a basis function that has one peak and two bottoms.

In short, as a generation, facing covid-19 in early career is hardly blessed. But it is like a “slightly increased risk” result from 23andme gene screening: set aside the non-changeable (I mean this is the time we are praying for a do operator) generation effect, there is much more else we can do.